Axiomatic Design Principles in the Context of Systems Engineering (Part 1 of 2)

ABSTRACT

Axiomatic design is the formalized process that allows for universal design axioms to be used by engineers for the conceptualization and embodiment of designs. To accomplish the axiomatic design, training is combined with design tools to create engineering specifications. Using tools such as design axioms, domain mapping, and systems modeling language, engineers can reduce design flow times while ensuring customer requirements are met to the greatest extent possible. Along with axiomatic design are other tools that allow for designers to adequately address stakeholder needs while maximizing the effectiveness of their product. This paper seeks to examine the modern usage of these design tools and review the literature on the topic.

INTRODUCTION

Systems can be described as any collection of subsystems, software, hardware, and personnel designed to perform tasks to meet functional requirements. These functional requirements are subject to constraints that may be physical, informational, or environmental. Whenever considering system design, one must consider how complex the system is, how complex should the system interrelations be, and how to control the system such that it consistently achieves its functional requirements. Additionally, human-machine interaction must also be considered[1].

With the advancement of systematic design, concurrent engineering, and many other design methodologies has come a need for relating customer needs to design requirements. In the embodiment phase of systematic design, requirements, and constraints must be determined [2]. Using axiomatic design principles, customer requirements can be mathematically related to design parameters. This allows for an improved system for understanding customer requirements and ensuring they are adequately met.

NOMENCLATURE
AM- Additive Manufacturing
CN - Customer Needs
DP - Design Parameters
ESM - Engineering System Matrix
FR - Functional Requirement
ICAD - International Conference on Axiomatic Design
INCOS - International Council on Systems Engineering
MBSE - Model-based Systems Engineering
SysML - Systems Markup Language
QFD - Quality Function Deployment
QKC - Qualitative Knowledge Construction
TRIZ - Theory of the Resolution of Invention-related Tasks

AXIOMATIC DESIGN FUNDAMENTALS

Axiomatic design is a formalized design methodology that makes use of universal engineering axioms to assist engineers in the creation of a system [3]. Axioms, universally applied concepts that are true without the burden of proof, are used in various engineering design systems.

Suh's concept of axiomatic design axioms differs from other methodologies in that the axioms are simultaneously simple and powerful tools that drive functional requirements and design parameters. Suh believed that a design could be no better than the sum of its functional requirements [4]. In other methodologies (such as Hazelrigg's axiomatic framework), axioms define self-evident principles strictly mathematically[5][6]. Instead, Suh sought to use two simple yet powerful axioms to drive manufacturing design toward an efficient solution.

Manufacturing systems are no longer immediately designed. Instead, they evolve from a series of design decisions that seek to match customer and functional requirements [7]. The axiomatic design seeks to codify this concept into a formalized process that allows for decisions to be produced because of rational design.

MATRIX OPERATIONS
In Axiomatic Design, matrix operations are used to analyze the relationship between customer needs and design parameters. Functional requirements are defined by weighting factors for each design parameter as shown in Equation 1. Weighting factors may be a Boolean True/False, integer value, or any other method of relating the variables.

Many designers use Boolean values to relate design parameters to functional requirements. This simplifies calculations as false results provide a zero result. An example of using Boolean values in the design matrix for a Beech Baron 58 tail-cone redesign can be shown in Figure 1 below [8].

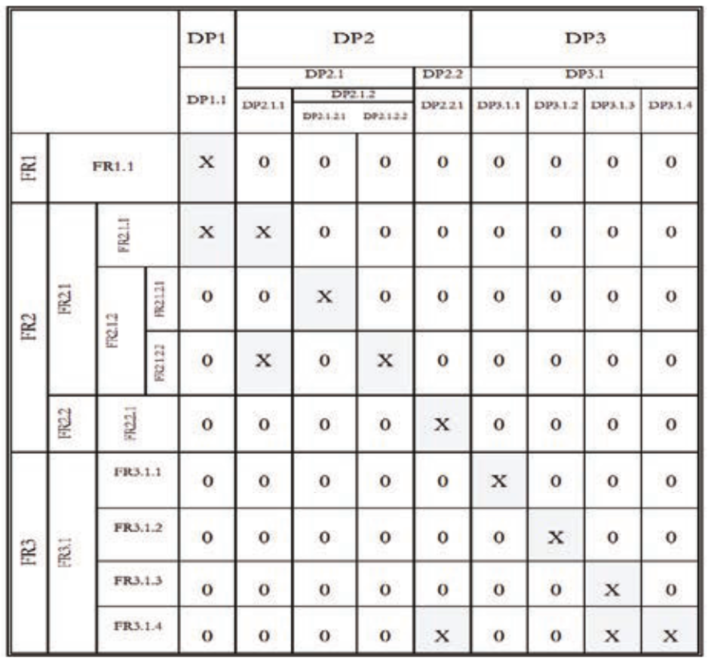
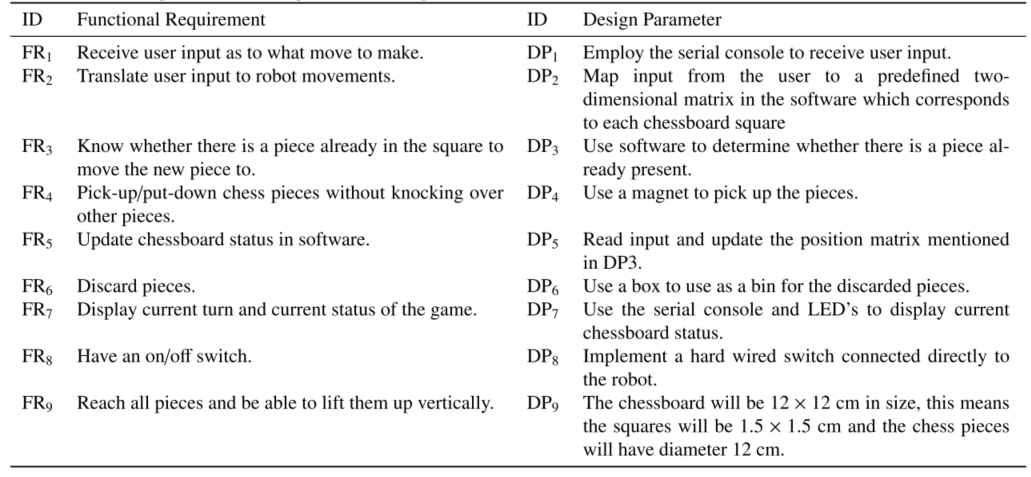
By decomposing design domains into hierarchical Functional Requirements and Design Parameters, a relationship can be formed between customer and design requirements after conducting the design matrix operation. Care must be taken to ensure that functional requirements are correctly defined at the correct level of hierarchy otherwise confusion in the mapping process may result [8] A list of example functional requirements and design parameters can be seen in Table 1.

The ad-hoc nature of decomposition lends itself to unreliable results. Insufficient decomposition will lead to errors. Similarly, too much decomposition results in violation of the Information Axiom which invalidates the result. A method of zigzagging between adjacent design domains is recommended to reduce errors and ensure that functional requirements, design parameters, and process variables are created in each major design domain [9].

INDEPENDENCE AXIOM

The Independence Axiom states that functional requirements must be independent of each other. This means that functional requirements must be both mutually exclusive and collectively exhaustive. The requirements of the design goals must be fully captured by the functional requirements [11].
By maintaining the Independence Axiom, no functional requirement mandates, including another functional requirement. Similarly, the converse is true. No functional requirement may exclude another requirement by requiring exclusive features [11].

As an example of the Independence Axiom in use, consider a supermarket. Two items that are typically bought are bread and milk. These items are placed on the opposite far ends of the supermarket. This maximizes the time spent in the store which has the net effect of maximizing exposure to other products.

If the functional requirements were to minimize walking time while maximizing time spent in the store, these functional requirements would violate the independence axiom. It can be inferred that maximizing time in the store was not a functional requirement. Instead, the functional requirements could be maximizing exposure to products while minimizing walking time [12].

INFORMATION AXIOM

The Information Axiom requires that the informational content of a design be minimized. This is accomplished by minimizing the range of potential design parameters. These parameters can be considered as x-direction ranges on a Gaussian curve where the probability of a set of ranges forms the dependent variable. The goal of the Information Axiom is to minimize the applicable area of the Gaussian curve [3].

To continue the supermarket analogy, a simple design tends to work best. To have the simplest design for the customer, a supermarket could be arranged like a Kanban work cell where the entrance and exits are on opposite ends of the building. A valet service moves the customer's car from the entrance lot to the egress lot. The path the customer takes maximizes their exposure to products to purchase while minimizing the chance of having to circle back. This would minimize the complexity of the customer path length [12].

Continue to Part 2 here